Summary:
With the development of power communication technologies, a large number of distributed power communication subsystems and massive power communication data have been produced, and it is very important to mine important information in massive data. As an effective method for data parallelization and information mining, cluster analysis has been widely used in power communication. However, traditional clustering algorithms can no longer meet the requirements of time performance when processing large amounts of power data. Aiming at this problem, a parallelized k-medoids clustering algorithm based on MapReduce model is proposed. Firstly, density-based clustering is used to optimize the initial point selection strategy of k-medoids algorithm, and MapReduce under Hadoop platform is used. The programming framework implements the parallelization of the algorithm. Experimental results show that compared with other algorithms, the improved parallel clustering algorithm reduces the clustering time, improves the clustering accuracy, and is conducive to the effective analysis and utilization of power data.
0 Preface
With the continuous development of function-centric electric power communication networks, a large number of O&M management systems have been developed with sub-professional, sub-function, and sub-management domains, which has led to the generation of large numbers of power data islands. How to use the distributed system to better deal with the large amount of data and complex types of power communication operation and maintenance data has become a hot topic of research. As an effective method of data processing, cluster analysis supports the integration and classification of a large number of unordered distributed data to perform deeper correlation analysis or data mining, and has been more and more widely used in power communication networks. At the same time, parallel processing mechanism in distributed systems has become an important research direction of data mining due to its excellent flexibility and high efficiency.
Scholars at home and abroad are increasingly paying more attention to this aspect. Literature [1] proposes a parallel optimization clustering algorithm based on DBSACN algorithm. In [2], the most central k data points are selected as the initial cluster centers by calculating the distance, and then iterative clustering is performed using the k-medoids algorithm, which improves the clustering effect, but is not suitable for processing large-scale data; the literature [3] An ant colony k-medoids fusion clustering algorithm is proposed. This algorithm does not need to determine the number of clusters and the initial clustering center artificially, which improves the clustering effect, but it is only applicable to small datasets. The literature [4] adopts it. Based on the clustering algorithm of granular computing, the computational complexity of the algorithm in the initial clustering center selection process is large, and there is a time delay problem in processing large-scale data; literature [5] proposes to embed the local search process into iterations. The method of local search significantly reduces the calculation time. [6] implemented the parallelization of traditional k-medoids clustering algorithm on the Hadoop platform, which reduced the clustering time, but did not improve the selection mechanism of the initial clustering center and did not improve the clustering effect; 7] The kernel-based adaptive clustering algorithm overcomes the initial sensitivity problem of k-medoids, but it does not reduce the time complexity of the algorithm.
In summary, the k-medoids clustering algorithm has the problems of initial value sensitivity, slow running speed, and high time complexity. It is necessary to optimize the algorithm for the initial point selection and parallelization in the k-medoids algorithm.
Improved mechanism of initial point selection for 1 k-medoids clustering
The k-medoids algorithm is a partition-based clustering algorithm, which has the advantages of simplicity, fast convergence, and insensitivity to noise points. Therefore, it has been widely used in pattern recognition, data mining and other fields. The initial center point of the k-medoids algorithm is very important. If the initial center point is an outlier, it will cause the centroid calculated by the outlier to deviate from the whole cluster, resulting in incorrect data analysis; if the selected initial center Too close to one point will significantly increase the time spent on calculations. Therefore, this algorithm first optimizes the selection of the initial center point. Density-based clustering can separate clusters and ambient noise very well, so this paper uses density-based clustering to minimize the impact of noise data on the selection of initial points.
Definition 1: The point density is the number of sample points contained in a spherical domain with x as the center of the sphere and a positive number r as the radius of the sample point x of the data set in the data set U, denoted as Dens(x). . among them:

In this algorithm, point density is first calculated for each data point in parallel, and point density is used as an attribute of the data point. The specific steps for selecting the initial cluster center are as follows:
(1) Calculate the distance between m data points in the data set.
(2) Calculate the dot density Dens(xi) and the mean dot density AvgDens for each sample point, store the point density that is greater than AvgDens, that is, the core point, into the set T, and record the data points contained in the cluster.
(3) Merge all clusters with common core points.
(4) Calculate the cluster density CDens(ci) of each cluster, select k clusters with larger density, and calculate the center point, which is the initial clustering center.
The cluster center point is calculated as follows: Assuming that a cluster ci contains m data points {x1,x2,...,xm}, the center point ni is calculated as in equation (5):

Through the above steps, the selection of the initial cluster center point can be optimized, the subsequent clustering iteration operation is more effective, the search scope is reduced, and the search assignment time is greatly reduced.
Parallel Design Strategy of 2 k-medoids Clustering Algorithm
In this paper, the k-medoids algorithm has the disadvantages of complex initial point selection, long clustering iteration time, and excessive consumption of center point selection. The MapReduce programming framework under the Hadoop platform is used to calculate the initial point point density of the algorithm. Improvements have been made in the parallelization of central point allocations and the parallelization of central point updates. MapReduce is divided into two parts: Map (map) and Reduce (reduce). The key to using MapReduce to implement the algorithm is to design the Map function and Reduce function. The Map function maps multiple tasks that can be executed in parallel to multiple compute nodes. Multiple compute nodes process parallel tasks that are assigned to each other. The Reduce function returns the results to the master after each compute node finishes processing. The process is summarized.
2.1 Point Density Parallelization Strategy
In the calculation of the dot density, since the dot density of one data point has no effect on the dot density of other data points, the calculation process can be parallelized. Use MultithreadedMapper to run multiple Mappers in a JVM process at the same time in a multi-threaded manner. Each thread instantiates a Mapper object, and each thread executes concurrently. The main process assigns the data points to several different computing nodes for processing. The computing node divides the data into k parts equally and has k threads. The data points in each thread are calculated with the distances of all the points in the data set, and then calculated. Out of the density, the final summary through the Reduce function results and output. The parallel processing makes the time used for point density calculation greatly reduced, and improves the execution efficiency of the algorithm.
2.2 Non-central point allocation and center point update parallelization strategy
The main task of the non-center distribution stage is to calculate the distance from each data point to each center point. Since the calculation of the distance between each data point and each center point does not affect each other, the calculation process can also be parallelized. In the MapReduce process of this stage, the Map function is mainly responsible for assigning each sample point in the data set except the center point to the nearest cluster center, and the Reduce function is responsible for updating the center point of each cluster by calculation, according to This principle is iterated until the set threshold is reached. The main process uses the Map function to assign tasks assigned to non-center points to a number of compute nodes. Each compute node employs a Round-Robin-based parallelized allocation strategy. First, consider each data point as a request, assign it to different threads in a polling manner, calculate the distance between the non-center point and each center point, find the minimum distance, and then assign the non-center point to the minimum distance. The corresponding center point.
Because the polling scheduling algorithm assumes that all servers have the same processing performance, they do not care about the current computing speed and response speed of each server. Therefore, when the user makes a request, if the time of the service interval changes greatly, the Round-Robin scheduling algorithm is very easy to cause the load imbalance between servers to perform. However, each data point used in this article is equal, so it will not cause the problem of uneven server assignment. Therefore, a Round-Robin-based strategy is feasible.
The algorithm in this paper has undergone two parallelizations in the process of clustering, which are non-center point allocation and center point updating process. The two parallelization processes are repeated until the conditions for exiting the program are satisfied.
3 Simulation experiment and result analysis
Simulation experiments were conducted using the algorithm, the DBSCAN parallelization algorithm [1] and the k-medoids parallelization algorithm [8], respectively, to compare and test the advantages and disadvantages of each algorithm. In order to prove the effectiveness of this algorithm, the experiment will analyze the clustering time, clustering accuracy of different algorithms and the time consumption after increasing the number of threads. The experiment will be tested on two types of datasets:
(1) Power data set. The properties of power communication data include device status, equipment assets, network topology, etc. The data volume is about 1 GB.
(2) Public data sets. They are Northix, on the order of 200, DSA on the order of 1 000, SSC on the order of 5,000, and GPSS on the order of 10 000.
3.1 Analysis of Power Dataset Experiment Results
The experiment first set 6 threads to process the data set. The results of the three algorithms for clustering power data are shown in Table 1. The k-medoids parallelization algorithm [8] adopts the label co-occurrence principle to improve the initial point selection, but does not consider the thread allocation method, so its execution efficiency is the worst; the DBSCAN algorithm takes into account the selection of the initial point and adopts dynamic allocation. The strategy is parallelized, but the consumption is increased in the process of calculating dynamic allocation. Therefore, the clustering accuracy and execution efficiency are slightly improved. The algorithm proposed in this paper not only considers the reasonable selection of the initial point, but also adopts a simple and effective method. Parallelization of the allocation strategy reduces computation and excessive resource consumption. As a result, the execution efficiency of the k-medoids parallelization algorithm and the DBSCAN parallelization algorithm is greatly improved, and the accuracy is also improved.
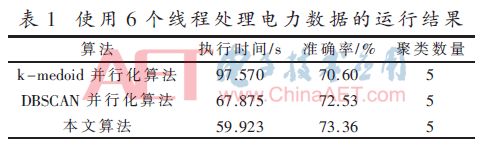
Then increase the number of thread processors to 8 to get the clustering results in the following table, see Table 2.
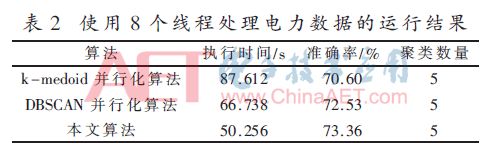
From Table 2, we can get, when using 8 threads, the performance of this algorithm is 42.64% faster than the k-medoids parallelization algorithm, and 24.70% faster than the DBSCAN parallelization algorithm.
The percentage of time spent by various algorithms to increase the thread compared to the original algorithm is shown in Figure 1.
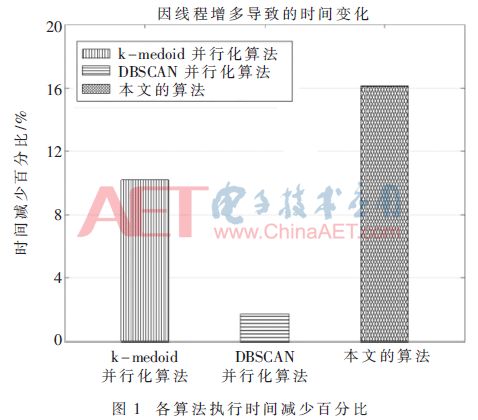
Figure 1 shows that the k-medoids parallelization algorithm is reduced by 10.20%, the DBSCAN parallelization algorithm is reduced by 1.68%, and the algorithm in this paper is reduced by 16.13%. This shows that the algorithm can reduce the operation time more effectively when the number of threads increases. effectiveness.
3.2 Analysis of Public Dataset Experiment Results
Based on the Northix, DSA, SSC, and GPSS data sets, the clustering accuracy of the algorithm using five threads is shown in Table 3.
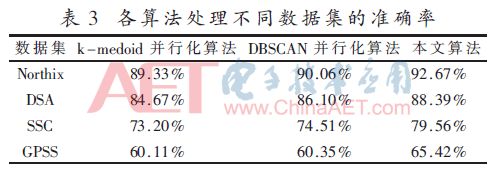
The clustering accuracy of this algorithm is higher than that of k-medoids parallel algorithm and DBSCAN parallel algorithm, and the accuracy of the algorithm is more dominant when dealing with data sets of a large number of orders. The execution time of each algorithm on different data sets is shown in Figure 2.
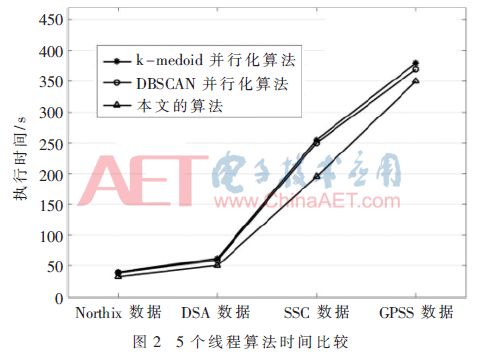
According to Fig. 2, as the amount of data increases, the difference in execution efficiency of the three algorithms gradually increases. The algorithm performance of this paper is obviously better than that of the k-medoids parallel algorithm and the DBSCAN parallel algorithm. Then compare the execution times when the three algorithms use 7 threads, as shown in Figure 3.
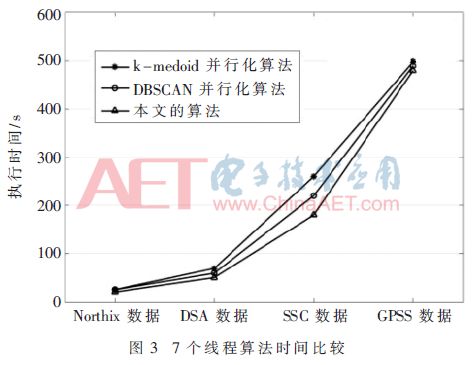
As can be seen from Figure 3, when using 7 threads at 1 000, 5 000, 10 000 data levels, the algorithm execution time of this paper is significantly better than the other two algorithms.
3.3 Experimental summary
Simulation experiments show that, when the number of threads is the same, the algorithm of this paper has higher clustering accuracy and shorter execution time than the comparison algorithm. When the number of threads increases, the execution time of the algorithm decreases significantly. With the increase of the data volume, the algorithm guarantees more. On the basis of high accuracy, the advantages of execution time are gradually highlighted.
4 Conclusion
For the problem of clustering processing of power communication data, this paper proposes a density-based clustering method to optimize the selection strategy of the initial point of the k-medoids algorithm, and uses the MapReduce programming framework to achieve the parallelization of the algorithm. Simulation experiments show that the proposed algorithm is feasible and effective, and has a good execution efficiency. In the next study, we can consider the optimal allocation strategy when the number of threads is less than the number of clusters, and further improve the performance of the algorithm.
Cbd Vape Products Oem,D8 Vape Pen Oem,Cbd Disposable Vape Pen Oem,China Cbd Vape Products Oem
Shenzhen MASON VAP Technology Co., Ltd. , https://www.masonvap.com