Image distortion often occurs in the process of actually acquiring and transmitting images, and the resulting image and the original image have some degree of difference. These are all because external noise is added to the image. Therefore, before processing the acquired image, it is necessary to pre-process the image, that is, to input the noise image.
Line filtering, smoothing the noise image. Traditional noise reduction methods include median filtering, mean filtering, and Wiener filtering. These methods have obvious limitations for non-stationary process signals.
Multiple image averaging methods are commonly used in video images of cameras to reduce the noise caused by TV camera optoelectronic camera tubes or CCD devices. This is to continuously capture multiple images and digitize the same scene, and then to multiple images.
Principle of multiple image averagingThe multi-image averaging method is to eliminate the noise by repeating the acquisition of the same scene for M times and then taking the average value. The image imaging model [4] can be described as:

It can be seen that the variance of the multi-image averaging method is M1 of the original image, and as M increases, the suppression of noise is stronger. The flow chart of this algorithm is shown in Figure 1.
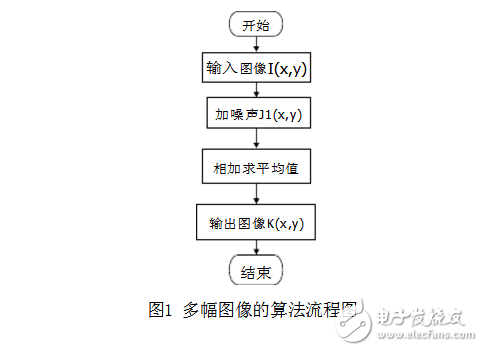
In the images captured by the camera, there is often some noise. This noise is generally uncorrelated in the spatial domain and is an additive noise. For an image captured by a camera, it can be expressed as a composition of noise-free images and additive noise, namely:
g(x,y)=f(x,y)+η(x,y)(1)
Where: g(x, y) is the acquired image, f(x, y) is the noiseless image, and η(x, y) is the noise.
The process of denoising is the process of approximating f(x, y) from the known g(x, y).
For multiple images taken in the same scene, fi(x, y) is the same, and ηi(x, y) is random and uncorrelated with each other, and the mean of k image images of the same scene can be expressed. as follows
g ̄(x,y)=1K∑i=1K[fi(x,y)+ηi(x,y)]=f(x,y)+1K∑i=1Kηi(x,y)(2)
Since the noise is random and irrelevant, the average image expectation is obtained.
E{g Ì„(x,y)}=f(x,y)(3)
Average image varianceΣ2g ̄(x,y)=1Kσ2η(x,y)(4)
which is
Σg ̄(x,y)=1K−−√ση(x,y)(5)
From equation (3) we can see that the expectation of the mean of multiple images of the same scene is a noise-free image, but there will be some disturbances, and the standard deviation of these disturbances (5) determines the intensity of the noise. The essence of our image denoising is to reduce the standard deviation in the spatial domain. From equation (5), we can easily find that by increasing the value of K, that is, increasing the number of average images, noise can be reduced.
But at the same time we can find: σâˆ1K√, ∂σ∂K=−12K3√, with the increase of K value, the change of σ becomes smaller and smaller, and when the average method is used for denoising, the effect of increasing the number of images alone It is very small.
Purpose
1. Verify that multi-image averaging in the same scene can be denoised.
2. As the number of images increases, image noise changes become smaller and smaller.
data set
179 photos of the same scene were collected in a short time.
Here is one of the pictures

Its partial details:

It can be found that there is more noise on the image.
programming
The processing of the program is:
* Read image
* Average
* Display image
Distribution Box,Industrial Distribution Box,Electricity Switch Box,Box For Distribution
Guangdong Shunde Langzhi Trading CO., Ltd , https://www.langzhielectrical.com